ホイールの話、前回からの続きです。
とりあえずスポークの長さを知りたいだけの方はネット上のスポーク長計算機を使用してください。
色々使ってみましたがスポーク長計算鬼 – 組 ま な い か –様が使いやすいです.
当記事ではスポーク長の計算結果というよりは計算の方法を解説します。
一般的なハブであればネット上のスポーク長計算機でいいのですが、特殊な形状のハブであったり、変則的な組み方をする場合には三平方の定理と余弦定理を駆使してスポークの長さを求める必要があります。
それでは、いってみましょう!
スポーク長を求めるのに必要な数値
スポーク長を求めるのに必要な数値があります。できれば小数点第一位まで(0.1mm)まで正確に測ると良いです。
①有効リム内径。組みあがった時にスポークの端が来る位置(ERD)
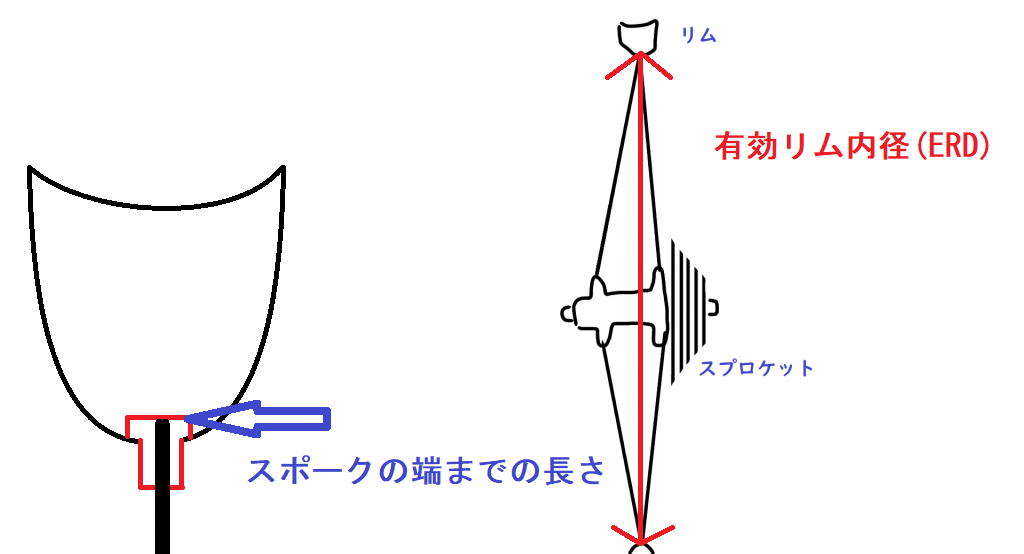
②ハブの中心からフランジまでの長さ。フランジ~センター(F~C)

③ハブのスポークを通す穴の直径(PCD)

④スポーク総数
⑤組み本数
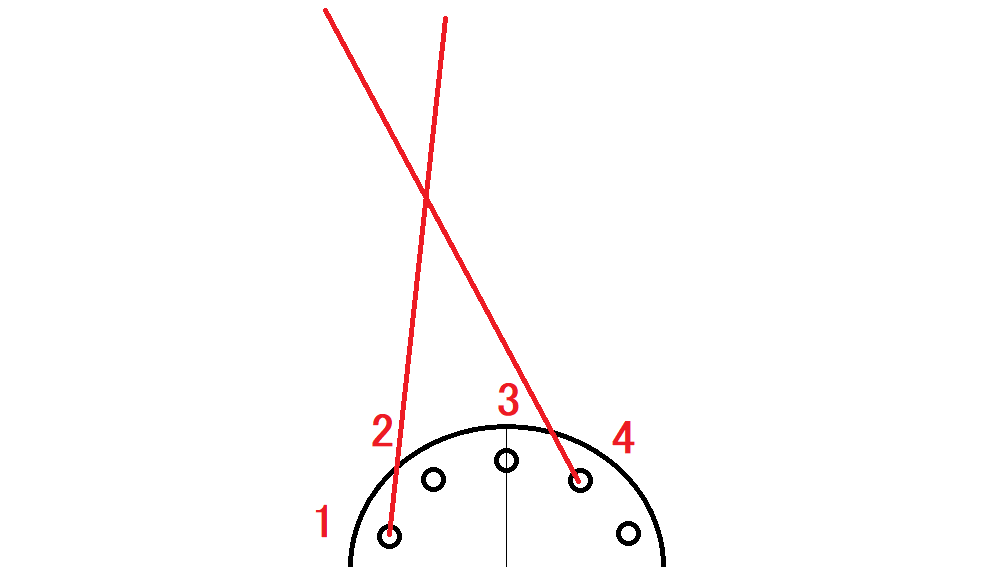
です。
ラジアル組みのスポーク長の求め方
下の写真がラジアル組みです。
まずはラジアル組みのスポーク長の求め方から解説します。

三平方の定理を使います。
三平方の定理とは、直角三角形の3辺の長さの関係を表す等式で、a²+b²=c²でしたね。
スポーク長の求め方は、有効リム内径の半径からフランジの高さを引いた寸法をa
フランジ~センターの寸法をbとします。
つまり
(ERD/2-PCD/2)²+F~C²=スポーク長²
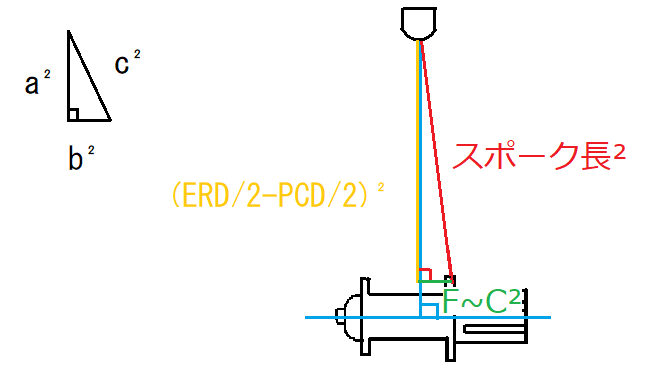
になります。(√をかけて戻すのを忘れないように)
タンジェント組みのスポーク長の求め方
次にタンジェント組みです。
タンジェント組みとは下の写真のような組み方です。交差組みとも言います。

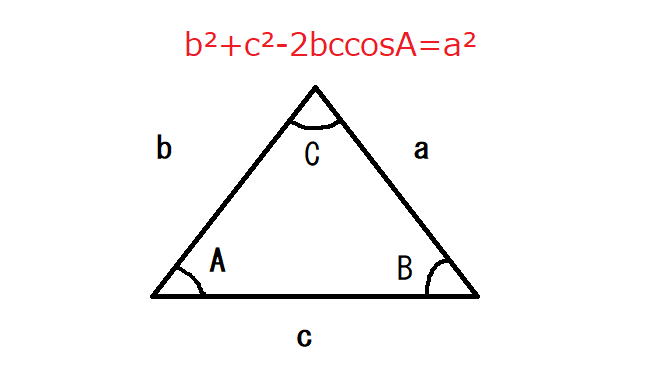
タンジェント組には余弦定理を使います。
余弦定理は、三角形の2辺の長さとその内角が分かれば残りの1辺の長さを求められる定理で、
b²+c²-2bccosA=a²でしたね。
ここでcosAをどうやって求めるかなんですが、
例えば32hハブと32hリムで組む事を考えてみましょう。
リムは360度の中に穴が32個あるので、隣同士の穴との角度は11.25度となります。
左右交互にスポークを通すので、穴は1個飛ばしで通しますので片側だけの隣を見ると22.5度ですね。
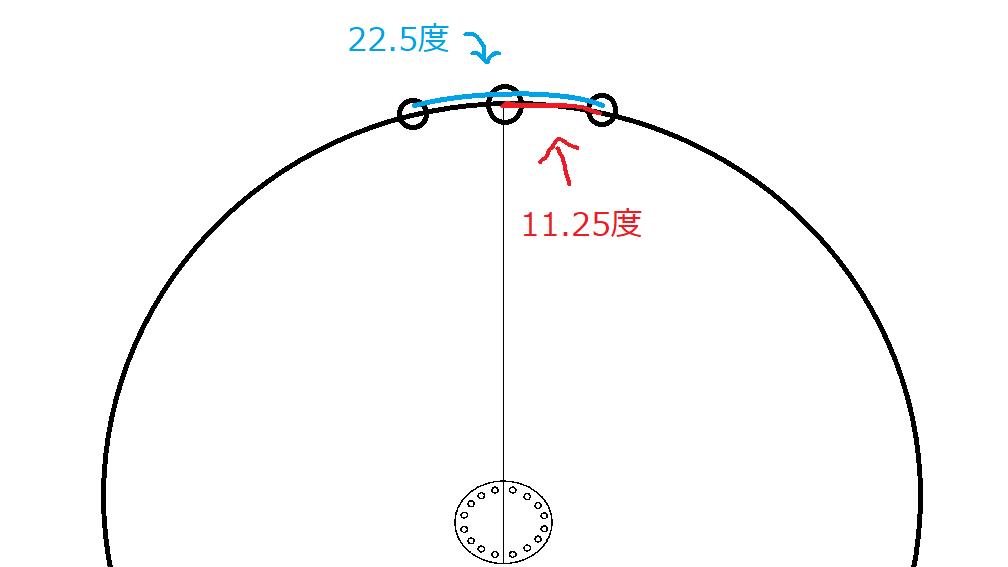
ハブは片側16個なので、隣同士の穴との角度は22.5度になりますね。
このようにスポークを通した時、ハブの頂点から一つ隣のスポーク穴まで11.25度となります。この穴をnとします。
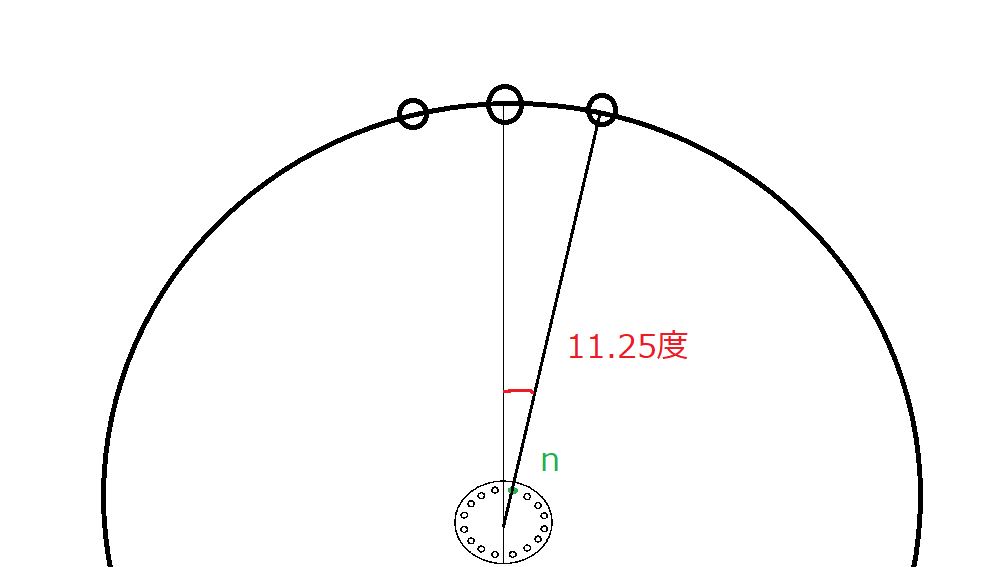
なので、リムからハブの中心までラジアル線を引くと、必ずnの穴の上をラジアル線が通ることになります。
そして、リム、ハブは動かさずに4本組、6本組、8本組をするとこうです。
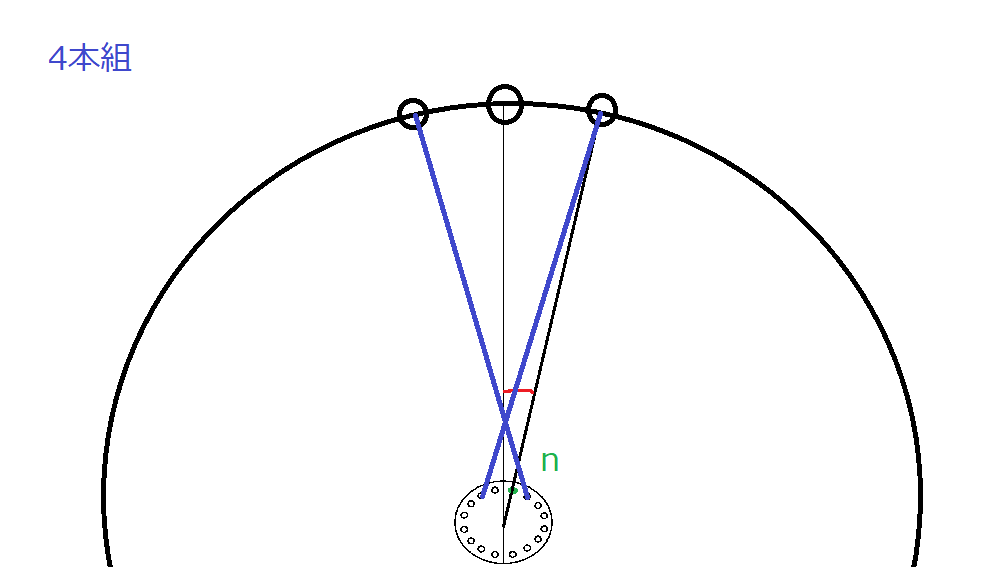
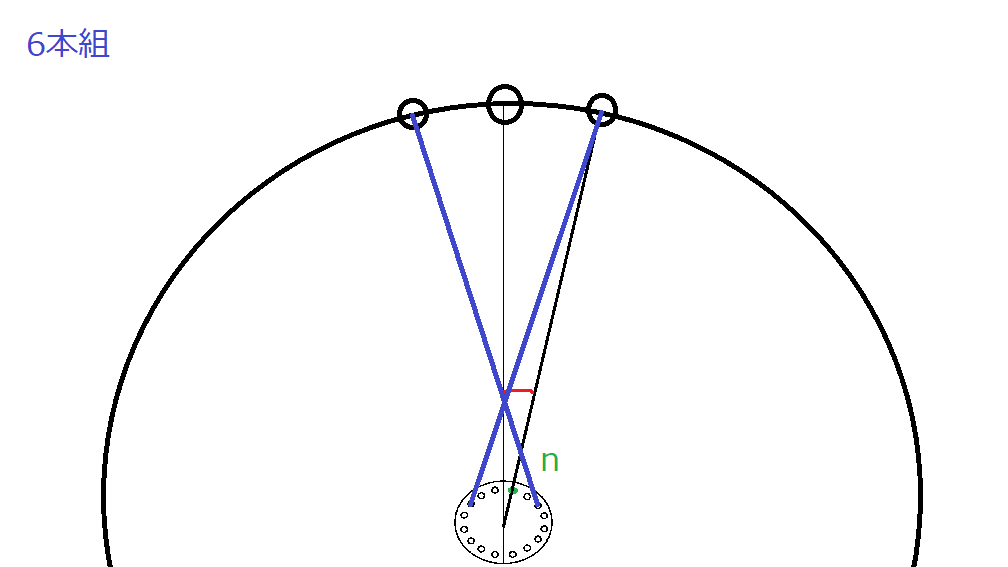
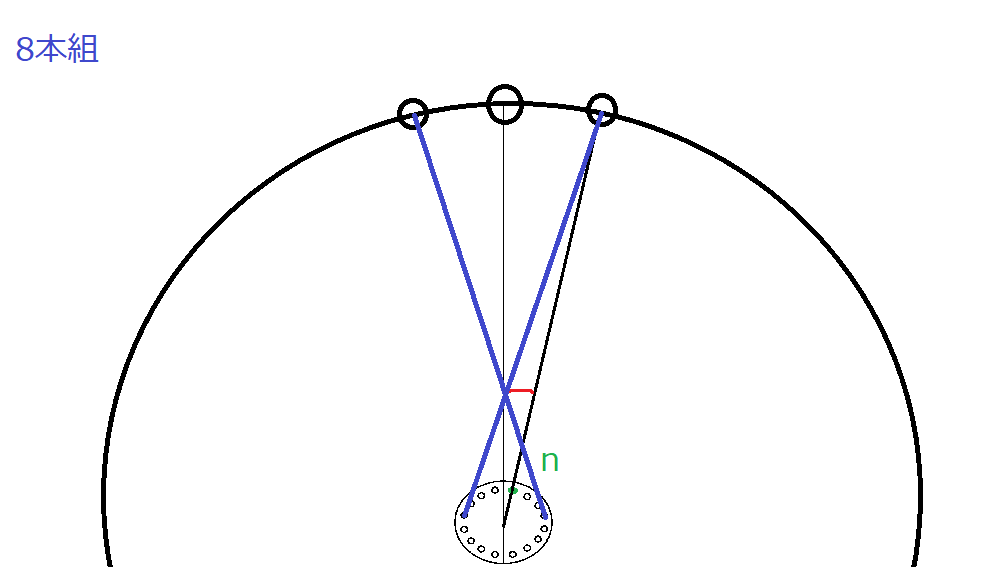
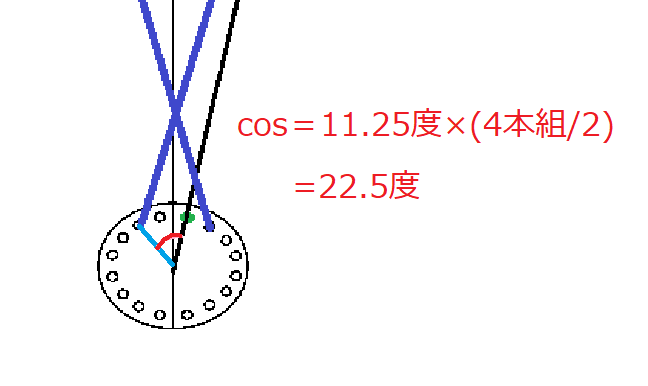
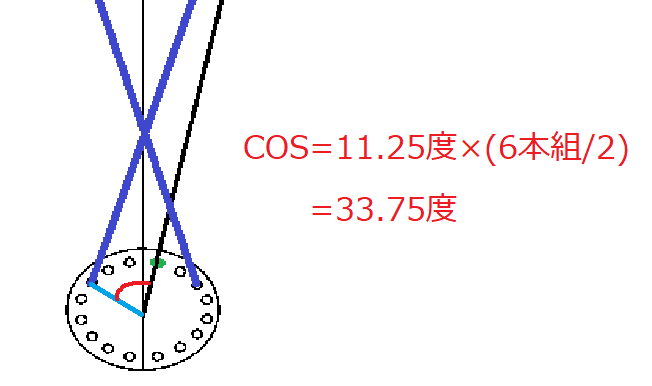
そこでcosを見てみると、組み本数/2となっている事が分かります。
4本組の場合
6本組の場合
8本組の場合
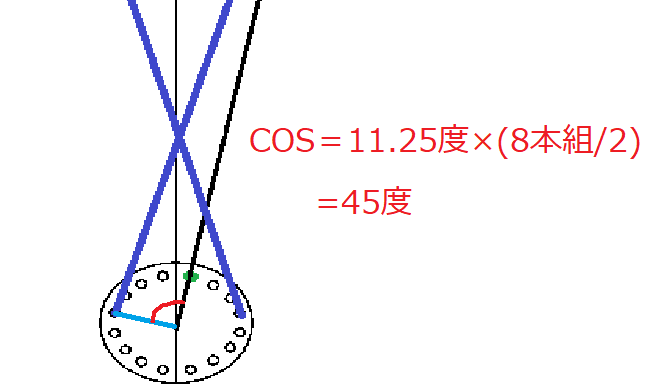
したがって、
(スポーク総数/360度)×(組み本数/2)=cosAになります。
PCDの半径をb、nを通るラジアル線をc、そしてcosAが揃いました。
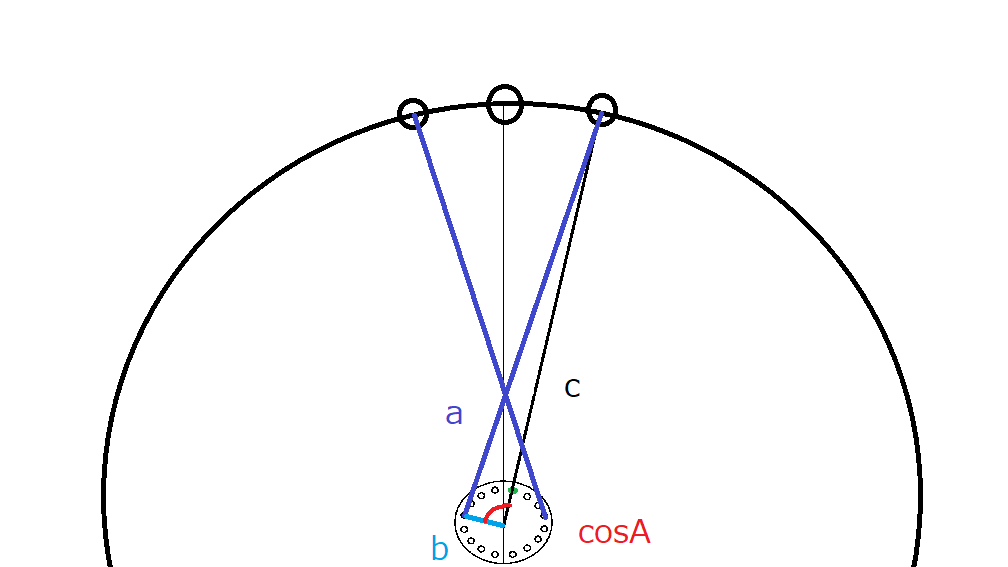
余弦定理の公式b²+c²-2bccosA=a²に代入すると
(PCD/2)²+(√((ERD/2)²+F~C²))²-2*(PCD/2)*(√(ERD/2)²+F~C²)*cos((スポーク総数/360度)*(組み本数/2))=スポーク長²
となります。
うーん。分かりやすく書こうと思ったら余計に分かりにくくなってしまったかも知れません。
こればっかりは自分で計算してみなければよくわからないと思います。
自分で計算してみてからこの記事を読み直せば、ああなるほど!となると思います。
ちなみにエクセルで上記の計算式を組めば、オリジナルのスポーク長計算機を作れます。
エクセルで使える関数のヒントだけ置いておきます
ルート:SQRT
COS:RADIANS
二乗:^2
です。
次回変則組みや特殊なハブのスポーク長の求め方へとつづきます。



