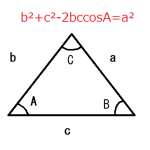
一般的なハブ、リムを使ってのスポーク長の求め方は前回の記事で紹介しました。
前回の記事の内容が理解できていなくても、一般的なハブやリムであれば、ネット上のスポーク長計算機を使って長さを知ることが出来ます。
今回は変則組み、特殊な構造のハブまたはリムで組む場合のスポーク長の求め方です。
三平方の定理と余弦定理をしっかり理解していないと出来ないので、前回の記事を参考にしてください。
ペアスポーク・粗密フランジ
ペアスポークとは下の写真のようなホイールで、左右のスポークがペアになっていて、間が開いている組み方です。

フランジの形状もリムに対応して広い部分と狭い部分がありますが、これを粗密フランジと言ったりします。
ごく稀に粗密フランジでない普通のハブで、ペアスポークを組んであるホイールが完成車に付いてくることがありますが、スポークが折れやすかったり緩みやすいようなまともなホイールでは無いので、早めに交換をおすすめします。
ペアスポークでもラジアルであれば計算に困りませんが、タンジェント組みの場合のスポーク長の求め方が問題ですよね。
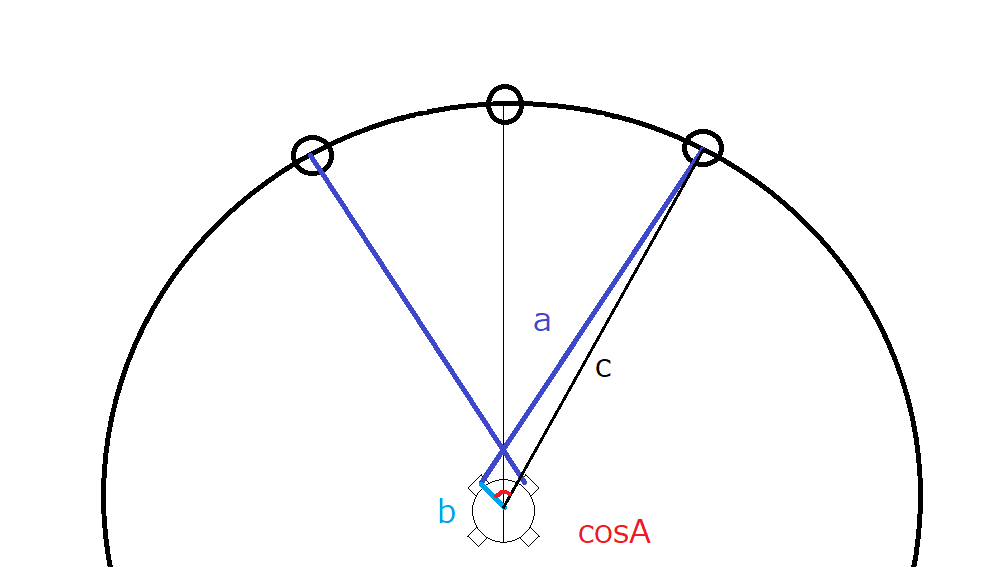
このbとcはいいとして、cosAの角度をどう求めるかが問題になってきます。
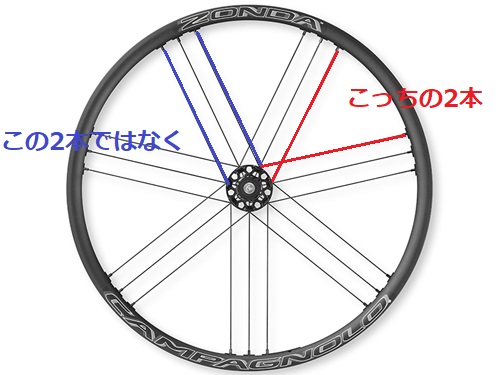
ややこしいのですが、ペアスポークというと一般的にはこの2本がペアですが、スポーク組みの観点でみるとペアは交差している2本です。

カンパのG3組のペアも一般的にはパラレルなこの2本がペアですが、スポーク組の観点では交差している2本がペアです。
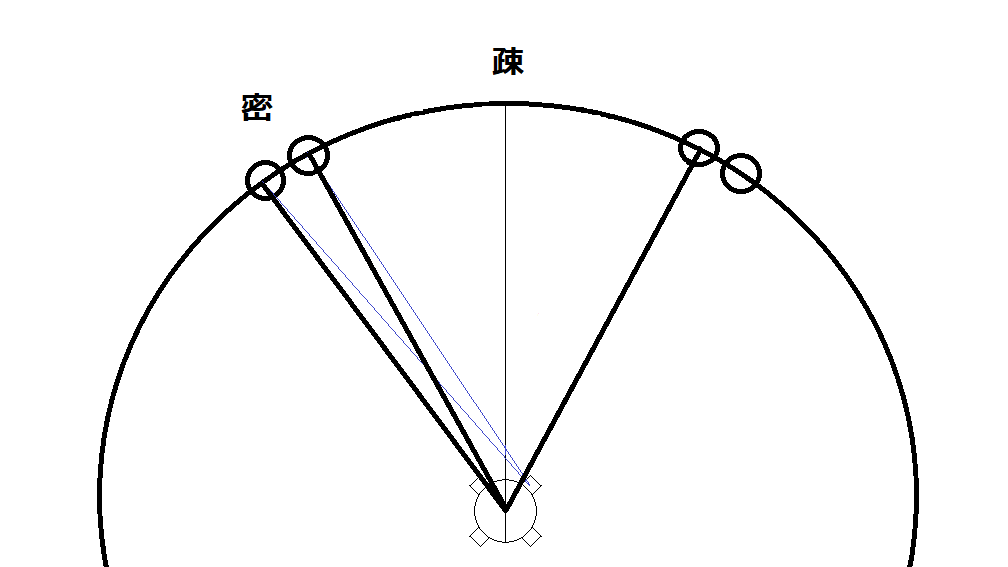
ペアスポークのニップルからハブ中心までのラジアル線の角度が分かればその右側と、ハブの左側の角度が分かれば出来そうですね。
ペアスポークの密な方の角度を求め、360度からその角度を引けば疎な方の角度が分かります。
扇の中心角を求める公式はx=180L/πrです。
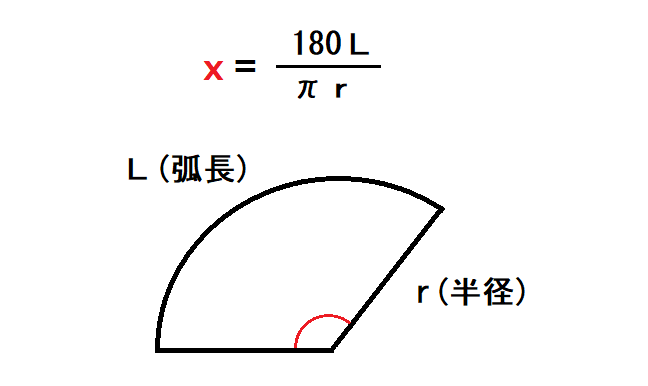
文字にすると中心角=(180*弧長)/(π*半径)ですね。
弧長を求めるのに弦長と半径から計算する公式もありますが、非常に挟角の為、誤差の範囲内なので弦長を使って大丈夫です。
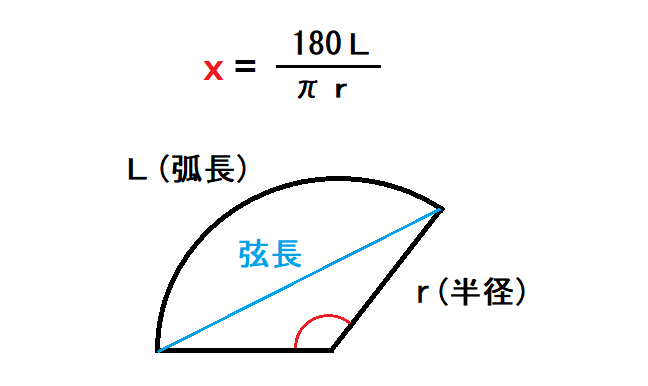
実際に計算してみましょう
このホイールでスポーク長を計算するとどうなるか、適当な数値を入れてやってみましょう。

仮にリム内径(有効リム内径でない)が550mm、密な弦長が10mmとすると
x=(180*10)/(3.14*275)
≒2.08
密が全部で8つあるので2.08*8=16.64
360-16.64=346.36
疎も全部で8つあるので346.36/8=43.295≒43.3
疎が43.3度と分かったので、その半分の21.65とします。
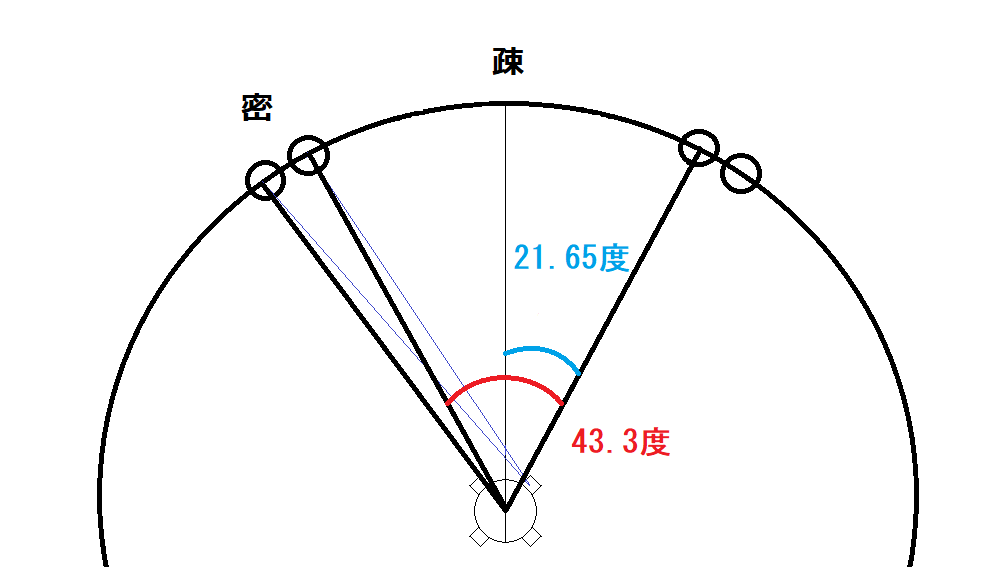
次にハブです。
ハブも同様に円周から密を引いて疎の角度を出します。
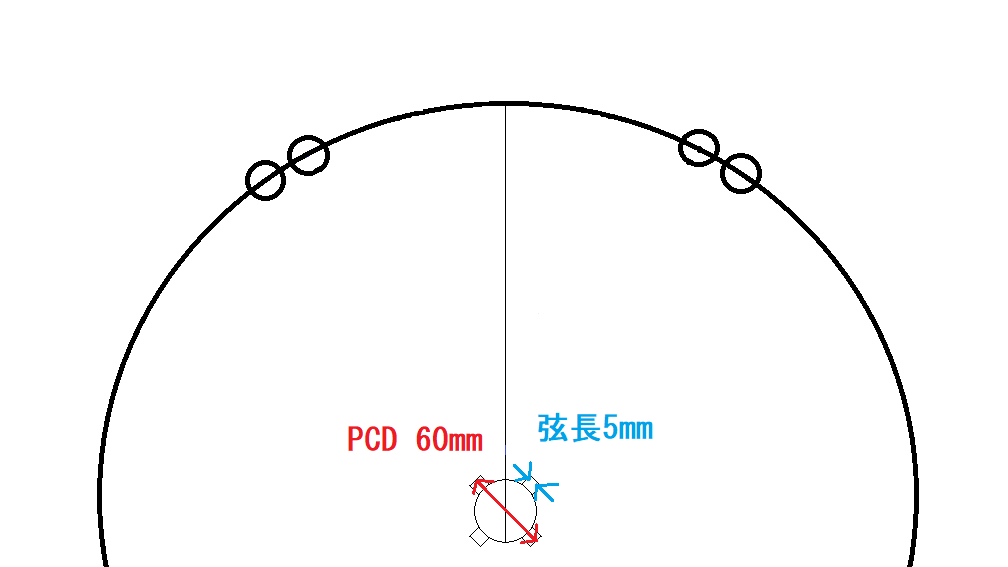
PCDが60mm、密な弦長が5mmとします。
密の角度は
x=(180*5)/(3.14*30)
=9.55
なので、
疎の角度=(360-(9.55*8))/8
=76.4
その半分で38.2
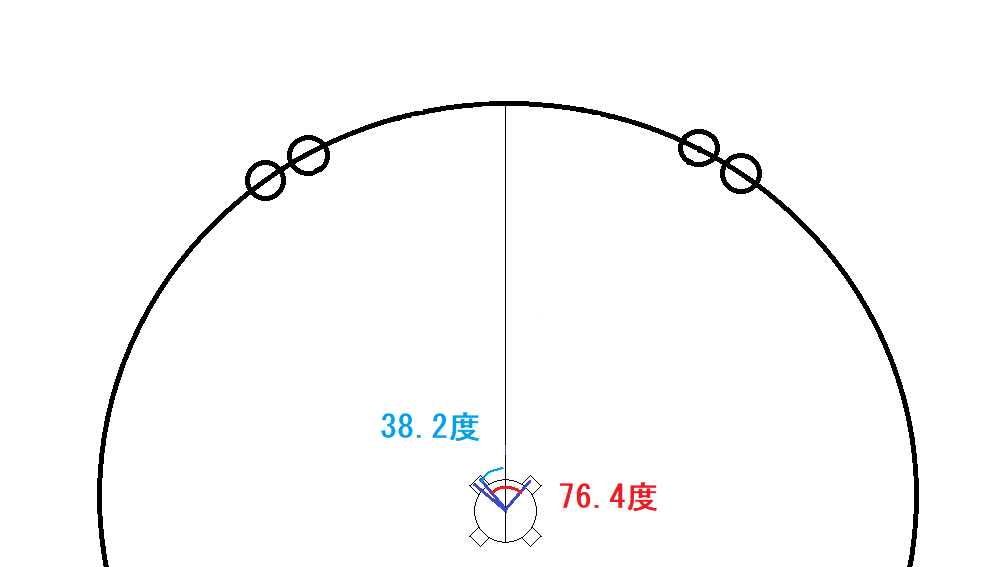
38.2+21.65=59.85≒60
cosAは60度とわかりました。
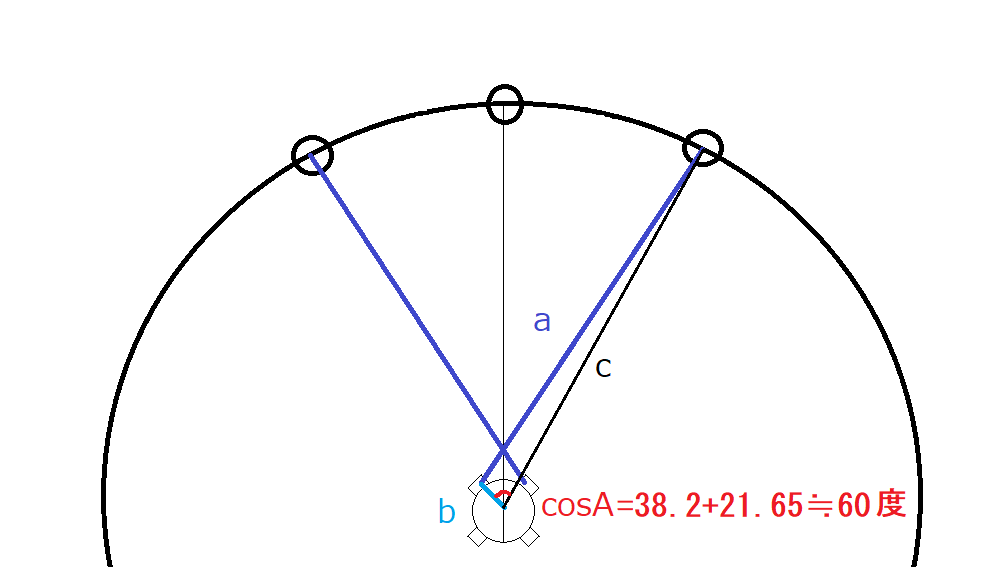
あとは余弦定理にあてはめて計算すればOKですね。
写真からの判断で適当に数字をあてはめてみましたが、近似値になったと思います。
特殊な形状のハブについても解説しようと思いましたが、長くなりすぎるので割愛します。
要はリムの穴とハブの穴の角度を求めて、その半分づつを足せばcosAを求めることができます。
まとめ
いかがでしたか?
スポーク長の計算は、やってみるのが一番です。
私自身も頑張って計算したのに、いざスポークを注文したら長さを間違っていた経験は何度もあります。
習うより慣れろですね。
ホイールの話はまだまだ続きます。
次回は良いホイールについて考えます。